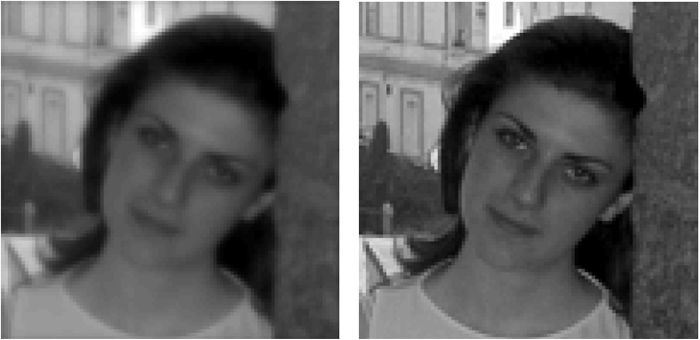Home About Research Publications Lectures Teaching Academic Collaborators Personalia
Topics
Projects







Blind source separation and deconvolution

Blind image separation and reflectance removal
Blind source separation for removal of reflections. Left: mixed images observed with different polarization. Center: separation result using the Farid-Adelson method. Right: sparse ICA results (Data by courtesy of Hany Farid)

Blind source separation (BSS) is a class of inverse problems, in which one wishes to separate a set of linearly mixed signals, having only the mixtures in hand and information neither about the sources, nor about the mixing coefficient. One-dimensional (1D) BSS problems arise in acoustics and communications; two-dimensional (2D) BSS problems arise, for example, in imaging through media with semireflective properties.


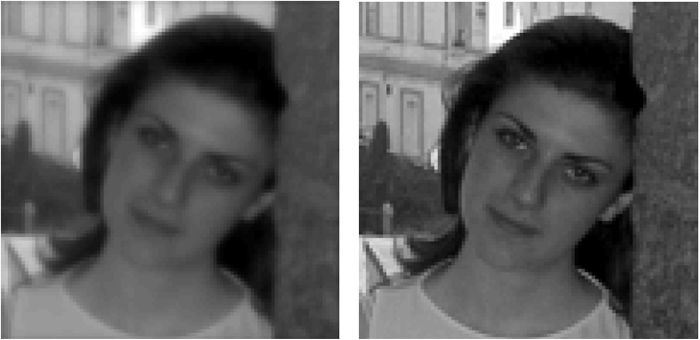
Blind deconvolution of Gabriella Sbordone's photo
Two-dimensional deconvolution example. Left: blurred image; Right: blind deconvolution result (Photo: Gabriella Sbordone)


Blind deconvolution (BD) is a family of inverse problems, in which one wishes to undo the action of an unknown linear shift-invariant system on an unknown input signal given only the output signal. Problems of this type often arise in communications and image processing.

Using the observation that many signals are sparse or sparsely-representable, very accurate and efficient separation and deconvolution can be performed using the relative Newton algorithm. We have developed an efficient block-coordinate version of the relative Newton optimization algorithm applicable to 1D and 2D sparse blind separation and deconvolution problems.

Papers

  • A. M. Bronstein, M. M. Bronstein, M. Zibulevsky, Y. Y. Zeevi, "Sparse ICA for blind separation of transmitted and reflected images", Intl. Journal of Imaging Science and Technology (IJIST), Vol. 15/1, pp. 84-91, 2005.

  • A. M. Bronstein, M. M. Bronstein, M. Zibulevsky, "Blind source separation using block-coordinate relative Newton method", Signal Processing, Vol. 84/8, pp. 1447-1459, August 2004.

  • M. M. Bronstein, A. M. Bronstein, M. Zibulevsky, Y. Y. Zeevi, "Blind deconvolution of images using optimal sparse representations", IEEE Trans. Image Processing, Vol. 14/6, pp. 726-736, June 2005.

  • A. M. Bronstein, M. M. Bronstein, M. Zibulevsky, "Relative optimization for blind deconvolution", IEEE Trans. Signal Processing, Vol. 53/6, pp. 2018-2026, June 2005.