| ||||||||||||||||||||
|
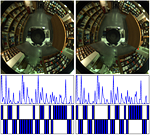
J. Masci, D. Migliore, M. M. Bronstein, J. Schmidhuber,
"Descriptor learning for omnidirectional image matching", chapter in Registration and Recognition in Images and Videos (R. Cipolla et al. Eds.), Springer, 2014 Abstract: Feature matching in omnidirectional vision systems is a challenging problem, mainly because complicated optical systems make the theoretical modelling of invariance and construction of invariant feature descriptors hard or even impossible. In this paper, we propose learning invariant descriptors using a training set of similar and dissimilar descriptor pairs. We use the similarity-preserving hashing framework, in which we are trying to map the descriptor data to the Hamming space preserving the descriptor similarity on the training set. A neural network is used to solve the underlying optimization problem. Our approach outperforms not only straightforward descriptor matching, but also state-of-the-art similarity-preserving hashing methods. |
|||||||||||||||||||
|
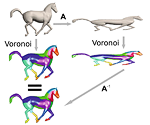
D. Raviv, A. M. Bronstein, M. M. Bronstein, R. Kimmel, N. Sochen,
"Equi-affine invariant geometries of articulated objects", chapter in Real-World Scene Analysis (F. Dellaert et al. Eds.), Springer, 2012. Abstract: We introduce an (equi-)affine invariant geometric structure by which surfaces that go through squeeze and shear transformations can still be properly analyzed. The definition of an affine invariant metric enables us to evaluate a new form of geodesic distances and to construct an invariant Laplacian from which local and global diffusion geometry is constructed. Applications of the proposed framework demonstrate its power in generalizing and enriching the existing set of tools for shape analysis. |
|||||||||||||||||||
|
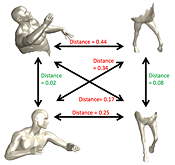
R. Litman, A. M. Bronstein, M. M. Bronstein,
"Stable semi-local features for non-rigid shapes", chapter in Innovations for Shape Analysis: Models and Algorithms (M. Breuss Ed.), Springer, 2012. Abstract: Feature-based analysis is becoming a very popular approach for geometric shape analysis. Following the success of this approach in image analysis, there is a growing interest in finding analogous methods in the 3D world. Maximally stable component detection is a low computation cost and high repeatability method for feature detection in images. In this study, a diffusion-geometry based framework for stable component detection is presented, which can be used for geometric feature detection in deformable shapes. The vast majority of studies of deformable 3D shapes models them as the two-dimensional boundary of the volume of the shape. Recent works have shown that a volumetric shape model is advantageous in numerous ways as it better captures the natural behavior of non-rigid deformations. We show that our framework easily adapts to this volumetric approach, and even demonstrates superior performance. A quantitative evaluation of our methods on the SHREC'10 and SHREC'11 feature detection benchmarks as well as qualitative tests on the SCAPE dataset show its potential as a source of high-quality features. Examples demonstrating the drawbacks of surface stable components and the advantage of their volumetric counterparts are also presented. |
|||||||||||||||||||
|
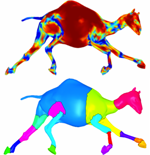
G. Rosman, M. M. Bronstein, A. M. Bronstein, A. Wolf, R. Kimmel,
"Group-valued regularization for motion segmentation of articulated shapes", chapter in Innovations for Shape Analysis: Models and Algorithms (M. Breuss Ed.), Springer, 2012. Abstract: Motion-based segmentation is an important tool for the analysis of articulated shapes. As such, it plays an important role in mechanical engineering, computer graphics, and computer vision. In this chapter, we study motion-based segmentation of 3D articulated shapes. We formulate motion-based surface segmentation as a piecewise-smooth regularization problem for the transformations between several poses. Using Lie-group representation for the transformation at each surface point, we obtain a simple regularized Ūtting problem. An Ambrosio-Tortorelli scheme of a generalized Mumford-Shah model gives us the segmentation functional without assuming prior knowledge on the number of parts or even the articulated nature of the object. Experiments on several standard datasets compare the results of the proposed method to state-of-the-art algorithms. |
|||||||||||||||||||

|
A. M. Bronstein, M. M. Bronstein, M. Ovsjanikov
"3D features, surface descriptors, and object descriptors", chapter in 3D Imaging, Analysis, and Applications (Y. Liu, N Pears, and P. Bunting Eds.), Springer, 2012. Abstract: The computer vision and pattern recognition communities have recently witnessed a surge of feature-based methods in numerous applications including object recognition and image retrieval. Similar concepts and analogous approaches are penetrating the world of 3D shape analysis, in a variety of areas including non-rigid shape retrieval and matching. In this chapter, we present the state-of-the-art of feature-based approaches in 3D shape analysis. |
|||||||||||||||||||
|
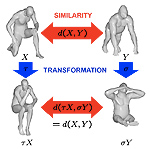
A. M. Bronstein, M. M. Bronstein,
"Manifold intrinsic similarity", chapter in Handbook of Mathematical Methods in Imaging (O. Scherzer Ed.), Springer, 2011. Abstract: Non-rigid shapes are ubiquitous in Nature and are encountered at all levels of life, from macro to nano. The need to model such shapes and understand their behavior arises in many applications in imaging sciences, pattern recognition, computer vision, and computer graphics. Of particular importance is understanding which properties of the shape are attributed to deformations and which are invariant, i.e., remain unchanged. This chapter presents an approach to non- rigid shapes from the point of view of metric geometry. Modeling shapes as metric spaces, one can pose the problem of shape similarity as the similarity of metric spaces and harness tools from theoretical metric geometry for the computation of such a similarity. |
|||||||||||||||||||

|
A. M. Bronstein, M. M. Bronstein, R. Kimmel,
"Story of Cinderella: biometrics and isometry-invariant distances", chapter in 3D Imaging for Safety and Security (A. Koschan, M. Pollefeys, M. Abidi Eds.), Springer, 2007. Abstract: In this chapter, we address the question of what are the facial measures one could use in order to distinguish between people. Our starting point is the fact that the expressions of our face can, in most cases, be modeled as isometries, which we validate empirically. Then, based on this observation, we introduce a technique that enables us to distinguish between people based on the intrinsic geometry of their faces. We provide empirical evidence that the proposed geometric measures are invariant to facial expressions and relate our findings to the broad context of biometric methods, ranging from modern face recognition technologies to fairy tales and biblical stories. |
|||||||||||||||||||

|
A. M. Bronstein, M. M. Bronstein, R. Kimmel,
"Expression invariant face recognition: faces as isometric surfaces", chapter in Face Processing: Advanced Modeling and Methods (R. Chellappa, W. Zhao Eds.), Academic Press, 2006. Abstract: One of the hardest problems in face recognition is dealing with facial expressions. Finding an expression-invariant representation of the face could be a remedy for this problem. We suggest treating faces as deformable surfaces in the context of Riemannian geometry, and propose to approximate facial expressions as isometries of the facial surface. This way, we can define geometric invariants of a given face under different expressions. One such invariant is constructed by isometrically embedding the facial surface structure into a low-dimensional flat space. Based on this approach, we built an accurate three-dimensional face recognition system that is able to distinguish between identical twins under various facial expressions. In this chapter we show how under the near-isometric model assumption, the difficult problem of face recognition in the presence of facial expressions can be solved in a relatively simple way. |
|||||||||||||||||||

|
A. M. Bronstein, M. M. Bronstein, M. Zibulevsky,
"Bind source separation: biomedical applications", article in Wiley Encyclopedia of Biomedical Engineering (M. Akay Ed.), April 2006. Abstract: Blind source separation (BSS) refers to a wide class of methods in signal and image processing, which extract the underlying sources from a set of mixtures without almost any prior knowledge about the sources nor about the mixing process. In biomedical applications, BSS is used for the analysis of electroencephalogram (EEG), magenetoencephalogram (MEG) and electrocardiogram (ECG) signals and functional magnetic resonance (fMRI) images. |
|||||||||||||||||||
|
| ||||||||||||||||||||